# 图
# 1. 定义
1、图:
多对多的网状结构,图 G 由两个集合 V (G) 和 E (G) 组成,记作:G=(V,E)。
**V(G) 是顶点的非空有限集合。
E(G) 是边的有穷集合,E (G) 可以是空集,如是空集则图 G 只有顶点没有边,而边是顶点偶对。
2、无向图:图 G 中的每条边都是没有方向的,通常用 ( ) 来表示。
3、有向图:图 G 中每条边都是有方向的,通常用 < > 来表示。
4、弧:有向边也称为弧。
5、弧尾:边的始点称为弧尾,或者初始点。
6、弧头:边的终点称为弧头,或者叫终端点。
7、n 表示顶点数,e 表示边数
无向图中边的数目为:0≤e≤n (n-1)/2 (另一半重复的原因),
有向图中边的数目为:0≤e≤n (n-1)
8、无向完全图:恰好有 n (n-1)/2 条边的无向图称为无向完全图。
9、有向完全图:恰好有 n (n-1) 条边的有向图称为有向完全图。
注意:完全图具有最多的边数。任意一对顶点间均有边相连。
10、图的边和顶点的关系
若 (vi,vj) 是一条无向边,则称顶点 vi 和 vj 互为邻接点 (Adjacent),或称 vi 和 vj 相邻接;
并称 (vi,vj) 依附或关联 (Incident)** 于顶点 vi 和 vj,或称 (vi,vj) 与顶点 vi 和 vj 相关联。
若 <vi,vj> 是一条有向边,则称顶点 vi 邻接到 vj,顶点 vj 邻接于顶点 vi;
并称边 <vi,vj> 关联于 vi 和 vj 或称 < vi,vj > 与顶点 vi 和 vj 相关联。
11、无向图中的度:顶点的度指依附于某顶点 v 的边数,通常记为 D (v)。
12、入度:顶点 v 的入度是指以顶点 v 为终点的弧的数目。记为:ID (v)
13、出度:顶点 v 的出度是指以顶点 v 为始点的弧的数目。记为:OD (v)
14、边、顶点、度之间的关系 (适应于有向图及无向图)
D (vi) 与顶点的个数以及边的数目满足关系:
E(G)=(D1+D2+….+Dn)/2
15、子图
在图 G=(V,E),G’=(V’,E’),若 V’∈ V,E’∈ E,且 E’中的边所关联的节点都在 V‘中,则 G’是 G 的子图。
(通俗来讲就是 G 包含 G')
16、路径 (有向图路径、无向图路径)
顶点 v 到 v‘的路径是一个顶点序列
路径长度:路径上边的数目。
17、回路:Vp=Vq 的路径,即起点和终点相同,也称环。
18、简单路径:该路径上除 Vp 和 Vq 可相同外,其余顶点均不相同。
19、连通、连通图、连通分量
连通:无向图中,若 vi 到 vj 有一条路径,则称 vi,vj 连通。
连通图:无向图中若对于任意两个不同的顶点 vi 和 vj 都连通,称 G 为连通图。例:无向图 G3 和无向图 G4 都是连通图
连通分量:无向图中 G 的最大连通子图称为 G 的连通分量。
20、强连通、强连通图、强连通分量
强连通:有向图中,vi –vj 及 vj—vi 都有路径,则 vi,vj 强连通。
强连通图:有向图中若对于作意两个不同的顶点 vi 和 vj 都存在从 vi 到 vj 及 vj 到 vi 的路径,则称 G 是强连通图。
强连通分量:有向图的极大强连通子图称为 G 的强连通分量。
任何强连通图的强连通分量只有一个,即是其自身。
非强连通的有向图有多个强连通分量。
21、生成树
一个连通图的生成树是一个极小连通子图。如果在一棵生成树上添加一条边,必定构成一个环。一棵有 N 个顶点的生成树有且仅有 N-1 条边。如果一个图有 N 个顶点和小于 N-1 条边,则是非连通图;如果多于 N-1 条边,则一定有环。有 N-1 条边的图不一定是生成树。
# 2. 存储结构
1. 邻接矩阵表示法
1) 基本思想
用一维数组存储图的顶点,用矩阵 (二维数组) 表示图中各顶点之间的邻接关系。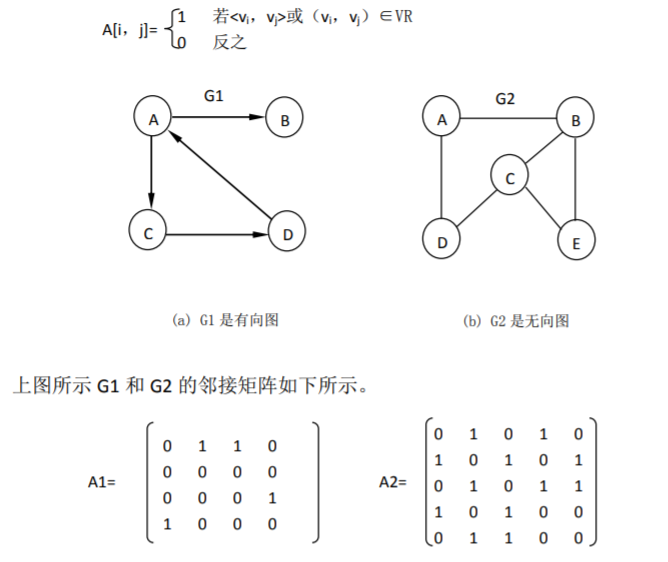
2) 邻接矩阵表示法的 C 语言描述如下
#define MAX_VERTEX_NUM 20 /* 最多顶点个数 */ | |
#define INFINITY 32768 /* 表示极大值,即∞*/ | |
/* 图的种类:DG 表示有向图,DN 表示有向网,UDG 表示无向图,UDN 表示无向网 */ | |
typedef enum{DG, DN, UDG, UDN} GraphKind; | |
typedef char VertexData; /* 假设顶点数据为字符型 */ | |
typedef struct ArcNode{ | |
AdjType adj; /* 对于无权图,用 1 或 0 表示是否相邻;对带权图,则为权值类型 */ | |
OtherInfo info; | |
} ArcNode; | |
typedef struct{ | |
VertexData vertex[MAX_VERTEX_NUM]; /* 顶点向量 */ | |
ArcNode arcs [MAX_VERTEX_NUM][MAX_VERTEX_NUM]; /* 邻接矩阵 */ | |
int vexnum, arcnum; /* 图的顶点数和弧数 */ | |
GraphKind kind; /* 图的种类标志 */ | |
}AdjMatrix; /*(Adjacency Matrix Graph) 邻接矩阵 */ | |
/* 求顶点位置函数 */ | |
int LocateVertex(AdjMatrix * G, VertexData v){ | |
int j=Error,k; | |
for(k=0;k<G->vexnum;k++) | |
if(G->vertex[k]==v){ | |
j=k; | |
break; | |
} | |
return(j); | |
} | |
int CreateDN(AdjMatrix *G){ /* 创建一个有向网 */ | |
int i,j,k,weight; VertexData v1,v2; | |
scanf("%d,%d",&G->arcnum,&G->vexnum); /* 输入图的顶点数和弧数 */ | |
for(i=0;i<G->vexnum;i++) /* 初始化邻接矩阵 */ | |
for(j=0;j<G->vexnum;j++) | |
G->arcs[i][j].adj=INFINITY; | |
for(i=0;i<G->vexnum;i++)scanf("%c",&G->vertex[i]); /* 输入图的顶点 */ | |
for(k=0;k<G->arcnum;k++){ | |
scanf("%c,%c,%d",&v1,&v2,&weight);/* 输入一条弧的两个顶点及权值 */ | |
i=LocateVex_M(G,v1); | |
j=LocateVex_M(G,v2); | |
G->arcs[i][j].adj=weight; /* 建立弧 */ | |
} | |
return(Ok); | |
} |
2. 邻接表表示法
1) 基本思想
只存储图中有关联的边的信息,对图中 n 个顶点均建立有关联的边链表
每个顶点信息与其边链表的头指针构成表头结点表
2) 结构构成
一个 N 个顶点的图的邻接表由表头结点表和边表两部分构成
表头结点表构成数据域 (vexdata)| 链域 (firstarc)
边标构成临界点域 (adjvex)| 链域 (nextarc)| 数据域 (info)
3) 邻接表存储结构的形式化说明如下:
#define MAX_VERTEX_NUM 20 /* 最多顶点个数 */ | |
typedef enum{DG, DN, UDG, UDN} GraphKind; /* 图的种类 */ | |
typedef struct ArcNode{ | |
int adjvex; /* 该弧指向顶点的位置 */ | |
struct ArcNode *nextarc; /* 指向下一条弧的指针 */ | |
OtherInfo info; /* 与该弧相关的信息 */ | |
} ArcNode; | |
typedef struct VertexNode{ | |
VertexData data; /* 顶点数据 */ | |
ArcNode *firstarc; /* 指向该顶点第一条弧的指针 */ | |
} VertexNode; | |
typedef struct{ | |
VertexNode vertex[MAX_VERTEX_NUM]; | |
int vexnum,arcnum; /* 图的顶点数和弧数 */ | |
GraphKind kind; /* 图的种类标志 */ | |
}AdjList; /* 基于邻接表的图 (Adjacency List Graph)*/ |

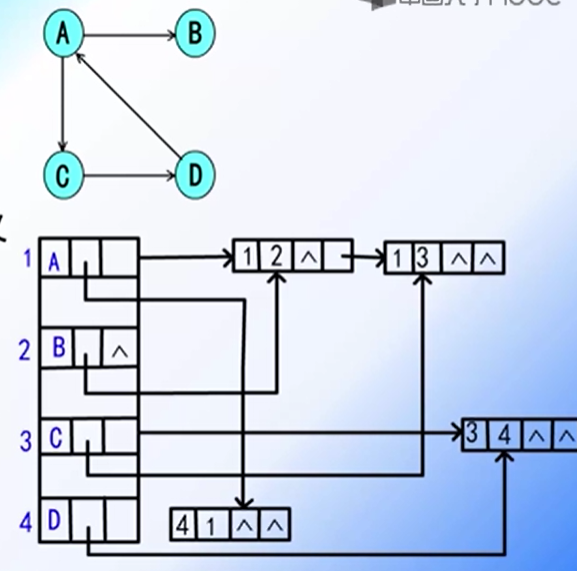
3. 十字链表
1) 定义
十字链表 (Orthogonal List) 是有向图的另一种链式存储结构。可以把它看成是 将有向图的邻接表和逆邻接表结合起来形成的一种链表。有向图中的每一条弧对应十字链表中的一个弧结点,同时有向图中的每个顶点在十字链表中对应有一个结点,叫做顶点结点。
2) 结构构成
十字链表由顶点结点和弧结点构成
顶点节点 data|| 链域 firstin
弧结点 弧尾结点 (tailvex) | 弧头结点 (headvex) | 头的下一条弧 (hlink) | 尾的下一条弧 (tlink)
4. 邻接多重表
邻接多重表 (Adjacency Multi_list) 是无向图的另外一种存储结构,邻接多重表是指将图中关于一条边的信息用一个结点来表示,
# 3. 图的遍历
与树的遍历相似,若从图中某顶点出发访遍图中每个顶点,且每个顶点仅访问一次,此过程称为图的遍历 (Traversing Graph)。
1. 深度优先遍历 (DFS)
1) 基本思想:给定一个连通子图,从图中某个结点 v1 出发,首先访问出发点 v1,然后选择一个 v1 的未被访问过的邻接点 v2,以 v2 为新的出发点继续进行深度优先遍历,当遇到一个所有邻接于它的顶点都被访问过时,则回到已访问顶点中最后一个拥有未被访问的相邻顶点,再进行深度优先,直至所有的顶点都被访问。直到子图中所有结点都被访问过 (递归定义)。若此时图中仍有未访问的结点,则另找一个连通子图,重复上述操作,直到图中所有的结点都被访问过。
特点:尽可能先对纵深方向进行搜索。
2) 算法实现
// 主函数 | |
void DFSTraverseAL(ALGraph *G){ | |
/* 深度优先遍历以邻接表存储的图 G*/ | |
int i; | |
for (i=0;i<G->n;i++)visited[i]=FALSE; | |
for (i=0;i<G->n;i++) | |
if (!visited[i]) DFS(G,i); | |
} | |
/* 以 Vi 为出发点对邻接表存储的图 G 进行 DFS 搜索 */ | |
void DFS(ALGraph *G,int i){ | |
EdgeNode *p; | |
//visit(v0); | |
printf("visit vertex:V%c\n",G->adjlist[i].vertex); /* 访问顶点 Vi*/ | |
visited[i]=1; | |
p=G->adjlist[i].firstedge; | |
while(p){ | |
if (visited[p->adjvex]==0){ | |
DFS(G,p->adjvex); | |
} | |
p=p->next;// 下一个邻接点 | |
} | |
} | |
// 用邻接矩阵方式实现深度优先搜索,图 g 为邻接矩阵类型 AdjMatrix | |
void DepthFirstSearch(AdjMatrix g, int v0){ | |
visit(v0); | |
visited[v0]=True; | |
for ( vj=0;vj<n;vj++) | |
if (!visited[vj] && g.arcs[v0][vj].adj==1) | |
DepthFirstSearch(g, vj); | |
}/* DepthFirstSearch */ | |
// 用邻接表方式实现深度优先搜索,图 g 为邻接表类型 AdjList | |
void DepthFirstSearch(AdjList g, int v0){ | |
visit(v0) ; | |
visited[v0]=True; | |
p=g.vertex[v0].firstarc; | |
while( p!=NULL ){ | |
if (! visited[p->adjvex]) | |
DepthFirstSearch(g, p->adjvex); | |
p=p->nextarc; | |
} | |
}/*DepthFirstSearch*/ |
2. 广度优先遍历
广度优先遍历 (Breadth_First Search) 是指按照广度方向搜索,它类似于树的层次遍历,是树的按层次遍历的推广。
1) 基本思想
(1) 从图中某个顶点 v0 出发,首先访问 v0。
(2) 依次访问 v0 的各个未被访问的邻接点。
(3) 分别从这些邻接点 (端结点) 出发,依次访问它们的各个未被访问的邻接点 (新的端结点)。访问时应保证:如果 Vi 和 Vk 为当前端结点,且 Vi 在 Vk 之前被访问,则 Vi 的所有未被访问的邻接点应在 Vk 的所有未被访问的邻接点之前访问。重复 (3),直到所有端结点均没有未被访问的邻接点为止。若此时还有顶点未被访问,则选一个未被访问的顶点作为起始点,重复上述过程,直至所有顶点均被访问过为止。
2) 算法实现
/* 广度优先搜索图 g 中 v0 所在的连通子图 */ | |
void BreadthFirstSearch(Graph g, int v0){ | |
visit(v0); | |
visited[v0]=True; | |
InitQueue(&Q); /* 初始化空队 */ | |
EnterQueue(&Q, v0); /* v0 进队 */ | |
while ( ! Empty(Q)){ | |
DeleteQueue(&Q, &v); /* 队头元素出队 */ | |
w=FirstAdjVertex (g, v); /* 求 v 的第一个邻接点 */ | |
while (w!=-1 ){ | |
if (!visited[w]){ | |
visit(w); | |
visited[w]=True;; | |
EnterQueue(&Q, w); | |
} | |
w=NextAdjVertex (g, v, w); /* 求 v 相对于 w 的下一个邻接点 */ | |
} | |
} | |
} |
# 4. 图的连通性
1. 无向图的连通分量
可以利用图的遍历过程来判断一个图是否连通。如果在遍历的过程中,不止一次调用搜索过程,则说明该图就是一个非连通图。几次调用搜索过程,表明该图就有几个连通分量。
2. 图中两个顶点之间的简单路径
在图的应用问题中,常常需要找从顶点 u 到另一个顶点 v 的简单路径,即路径中的顶点均不相同。u 到 v 可能存在多条简单路径,由于遍历过程将走遍图中的所有顶点,故可以在深度 (或广度) 优先搜索算法基础上加以适当的条件,就能得到求解此问题的算法,因此可以将此问题看成是有条件的图遍历过程。
// 深度优先找出从顶点 u 到 v 的简单路径 | |
int *pre; | |
/* 在连通图 G 中找一条从第 u 个顶点到 v 个顶点的简单路径 */ | |
void one_path(Graph *G, int u, int v){ | |
int i; | |
pre=(int *)malloc(G->vexnum*sizeof(int)); | |
for(i=0;i<G->vexnum;i++) pre[i]=-1; | |
pre[u]=u; /* 将 pre [u] 置为非 - 1,表示第 u 个顶点已被访问 */ | |
DFS_path(G, u, v); /* 用深度优先搜索找一条从 u 到 v 的简单路径。*/ | |
free(pre); | |
} | |
/* 在连通图 G 中用深度优先搜索策略找一条从 u 到 v 的简单路径。*/ | |
void DFS_path(Graph *G, int u, int v){ | |
int j; | |
if(pre[v]!=-1) | |
for(j=firstadj(G,u);j>=0;j=nextadj(G,u,j)) | |
if(pre[j]==-1){ | |
pre[j]=u; | |
if(j==v) print_path(pre ,v); /* 输出路径 */ | |
else DFS_path(G,j,v); | |
} | |
} |
3. 图的生成树与最小生成树
1) 生成树
图的极小连通子图。即:对于有 n 个顶点的无向连通图,无论其生成树的形态如何,所有生成树中都有且仅有 n-1 条边。
2) 最小生成树
在一个连通网的所有生成树中,各边的代价之和最小的那棵生成树称为该连通网的最小代价生成树 (Minimum Cost Spanning Tree),简称为最小生成树 (MST)。
3) 最小生成树方法
1. 普里姆 (prim) 算法
假设 G=(V,E) 为一网图,其中 V 为网图中所有顶点的集合,E 为网图中所有带权边的集合。设置两个新的集合 U 和 T,其中集合 U 用于存放 G 的最小生成树中的顶点,集合 T 存放 G 的最小生成树中的边。令集合 U 的初值为 U={u1}(假设构造最小生成树时,从顶点 u1 出发),集合 T 的初值为 T={}
Prim 算法的思想是,从所有 u∈U,v∈V-U 的边中,选取具有最小权值的边 (u,v),将顶点 v 加入集合 U 中,将边 (u,v) 加入集合 T 中,如此不断重复,直到 U=V 时,最小生成树构造完毕,这时集合 T 中包含了最小生成树的所有边。
通俗来讲就是,根目录下,找到每一个权值最小的边,把边连接起来,不要相互连通。

struct { | |
VertexData adjvex; | |
int lowcost; | |
} closedge[MAX_VERTEX_NUM]; /* 求最小生成树时的辅助数组 */ | |
/* 从顶点 u 出发,按普里姆算法构造连通网 gn 的最小生成树,并输出生成树的每条边 */ | |
void MiniSpanTree_Prim(AdjMatrix gn, VertexData u){ | |
k=LocateVertex(gn, u); | |
closedge[k].lowcost=0; /* 初始化,U={u} */ | |
for (i=0; i<gn.vexnum; i++) | |
/* 对 V-U 中的顶点 i,初始化 closedge [i]*/ | |
if ( i!=k){ | |
closedge[i].adjvex=u; | |
closedge[i].lowcost=gn.arcs[k][i].adj; | |
} | |
/* 找 n-1 条边 (n= gn.vexnum) */ | |
for (e=1; e<=gn.vexnum-1; e++){ | |
k0=Minium(closedge); /* closedge [k0] 中存有当前最小边 (u0,v0) 的信息 */ | |
u0= closedge[k0].adjvex; /* u0∈U*/ | |
v0= gn.vertex[k0] /* v0∈V-U*/ | |
printf(u0, v0); /* 输出生成树的当前最小边 (u0,v0)*/ | |
closedge[k0].lowcost=0; /* 将顶点 v0 纳入 U 集合 */ | |
for ( i=0 ;i<vexnum;i++) /* 在顶点 v0 并入 U 之后,更新 closedge [i]*/ | |
if ( gn.arcs[k0][i].adj <closedge[i].lowcost){ | |
closedge[i].lowcost= gn.arcs[k0][i].adj; | |
closedge[i].adjvex=v0; | |
} | |
} | |
} |
2. 克鲁斯卡尔 (Kruskal) 算法
算法思想
①首先构造一个只有 n 个顶点但没有边的非连通图 T={V,}, 图中每个顶点自成一个连通分量。
②当在边集 E 中选到一条具有最小权值的边时,若该边的两个顶点落在 T 中不同的连通分量上,则将此边加入到生成树的边集合 T 中;否则将此边舍去,重新选择一条权值最小的边。
③如此重复下去,直到所有顶点在同一个连通分量上为止。此时的 T 即为所求。
# 5. 有向无环图应用
有向无环图 (Directed Acyclic Graph):
是指一个无环的有向图,简称 DAG。有向无环图可用来描述工程或系统的进行过程,如一个工程的施工图、学生课程间的制约关系图等。
1. 拓扑排序 (Topological Sort):
用顶点表示活动,用弧表示活动间的优先关系的有向无环图,称为顶点表示活动的网 (Activity On Vertex Network), 简称为 AOV - 网。
拓扑排序的基本思想为:
(1) 从有向图中选一个无前驱的结点输出;
(2) 将此结点和以它为起点的边删除;
(3) 重复 (1)、(2),直到不存在无前驱的结点;
(4) 若此时输出的结点数小于有向图中的顶点数,则说明有向图中存在回路,否则输出的顶点的顺序即为一个拓扑序列。
算法实现:
(1) 基于邻接矩阵表示的存储结构
A 为有向图 G 的邻接矩阵,则有:
找 G 中无前驱的结点 —— 在 A 中找到值全为 0 的列;
删除以 i 为起点的所有弧 —— 将矩阵中 i 对应的行全部置为 0。
算法步骤如下:
①取 1 作为第一新序号;
②找一个未新编号的、值全为 0 的列 j,若找到则转③;否则,若所有的列全部都编过号,排序结束;若有列未曾被编号,则该图中有回路;
③输出列号对应的顶点 j,把新序号赋给所找到的列;
④将矩阵中 j 对应的行全部置为 0;
⑤新序号加 1,转②;
(2) 基于邻接表的存储结构
(1) 首先求出各顶点的入度,并将入度为 0 的顶点入栈;
(2) 只要栈不空,则重复下面处理:
①将栈顶顶点 i 出栈并打印;
②将顶点 i 的每一个邻接点 k 的入度减 1,如果顶点 k 的入度变为 0,则将顶点 k 入栈。
// 拓扑排序算法 | |
int TopoSort (AdjList G){ | |
Stack S; | |
int indegree[MAX_VERTEX_NUM]; | |
int i, count, k; | |
ArcNode *p; | |
FindID(G,indegree); /* 求各顶点入度 */ | |
InitStack(&S); /* 初始化辅助栈 */ | |
for(i=0;i<G.vexnum;i++) | |
if(indegree[i]==0) Push(&S,i); /* 将入度为 0 的顶点入栈 */ | |
count=0; | |
while(!IsEmpty(S)){ | |
Pop(&S,&i); | |
printf("%c", G.vertex[i].data); | |
count++; /* 输出 i 号顶点并计数 */ | |
p=G.vertex[i].firstarc; | |
while(p!=NULL){ | |
k=p->adjvex; | |
indegree[k]--; /*i 号顶点的每个邻接点的入度减 1*/ | |
if(indegree[k]==0) Push(&S, k); /* 若入度减为 0,则入栈 */ | |
p=p->nextarc; | |
} | |
} | |
if (count<G.vexnum) return(Error); /* 该有向图含有回路 */ | |
else return(Ok); | |
} | |
/* 求各顶点的入度 */ | |
void FindID( AdjList G, int indegree[MAX_VERTEX_NUM]){ | |
int i; ArcNode *p; | |
for(i=0; i<G.vexnum; i++)indegree[i]=0; | |
for(i=0; i<G.vexnum; i++){ | |
p=G.vertex[i].firstarc; | |
while(p!=NULL){ | |
indegree[p->adjvex]++; | |
p=p->nextarc; | |
} | |
} | |
} |
2. 关键路径
(理解)
通常用有向图来表示工程计划时有两种方法:
(1) 用顶点表示活动,用有向弧表示活动间的优先关系,即上节所讨论的 AOV 网。
(2) 用顶点表示事件,用弧表示活动,弧的权值表示活动所需要的时间。把用第二种方法构造的有向无环图叫做边表示活动的网 (Activity On Edge Network), 简称 AOE - 网。
源点:在 AOE 网中存在惟一的、入度为 0 的顶点;
汇点:存在惟一的、出度为 0 的顶点;
关键路径:从源点到汇点的最长路径的长度即为完成整个工程任务所需的时间。
关键活动:关键路径上的活动,这些活动中的任意一项活动未能按期完成,则整个工程的完成时间就要推迟。
在讨论关键路径算法之前,首先给出几个重要的定义:
(1) 事件 vi 的最早发生时间 ve (i):从源点到顶点 vi 的最长路径的长度,叫做事件 vi 的最早发生时间。
(2) 事件 vi 的最晚发生时间 vl (i):在保证汇点按其最早发生时间发生这一前提下,求事件 vi 的最晚发生时间。在求出 ve (i) 的基础上,可从汇点开始,按逆拓扑顺序向源点递推,求出 vl (i);
(3) 活动 ai 的最早开始时间 e (i):如果活动 ai 对应的弧为,则 e (i) 等于从源点到顶点 j 的最长路径的长度,即:e (i)=ve (j)
(4) 活动 ai 的最晚开始时间 l (i):如果活动 ai 对应的弧为,其持续时间为 dut () 则有:l (i)=vl (k)- dut () 即在保证事件 vk 的最晚发生时间为 vl (k) 的前提下,活动 ai 的最晚开始时间为 l (i)。
(5) 活动 ai 的松弛时间 (时间余量):ai 的最晚开始时间与 ai 的最早开始时间之差:l (i)- e (i)。显然,松弛时间 (时间余量) 为 0 的活动为关键活动。
求关键路径的基本步骤如下:
①对图中顶点进行拓扑排序,在排序过程中按拓扑序列求出每个事件的最早发生时间 ve (i);
②按逆拓扑序列求每个事件的最晚发生时间 vl (i);
③求出每个活动 ai 的最早开始时间 e (i) 和最晚发生时间 l (i);
④找出 e (i)=l (i) 的活动 ai,即为关键活动。
// 关键路径算法 | |
int CriticalPath(AdjList G){ | |
ArcNode *p; | |
int i,j,k,dut,ei,li; char tag; | |
int vl[MAX_VERTEX_NUM]; /* 每个顶点的最迟发生时间 */ | |
Stack T; | |
if(!TopoOrder(G, &T)) return(Error); | |
/* 将各顶点事件的最迟发生时间初始化为汇点的最早发生时间 */ | |
for(i=0; i<G.vexnum; i++) | |
vl[i]=ve[G.vexnum-1]; | |
/* 按逆拓扑顺序求各顶点的 vl 值 */ | |
while(!IsEmpty(&T)){ | |
Pop(&T,&j); | |
p=G.vertex[j].firstarc; | |
while(p!=NULL){ | |
k=p->adjvex; | |
dut=p->weight; | |
if(vl[k]-dut<vl[j]) vl[j]= vl[k]-dut; | |
p=p->nextarc; | |
} | |
} | |
/* 求 ei,li 和关键活动 */ | |
for(j=0;j<G.vexnum;j++){ | |
p=G.vertex[j].firstarc; | |
while(p!=NULL){ | |
k=p->Adjvex; | |
dut=p->Info.weight; | |
ei=ve[j];li=vl[k]-dut; | |
tag = (ei==li) ? '*' : ' ' ; /* 标记并输出关键活动 */ | |
printf("%c,%c,%d,%d,%d,%c\n",G.vertex[j].data,G.vertex[k].data,dut,ei,li,ta | |
g); | |
p=p->nextarc; | |
} | |
} | |
return(Ok); | |
} /*CriticalPath*/ |
# 6. 最短路径
1、带权图的最短路径:求两个顶点间长度最短的路径。其中:路径长度不是指路径上边数的总和,而是指路径上各边的权值总和。路径长度的具体含义取决于边上权值所代表的意义。
2、单源最短路径问题:已知有向带权图 (简称有向网) G=(V,E),找出从某个源点 s∈V 到 V 中其余各顶点的最短路径。
3. 迪杰斯特拉 (Dijkstra) 算法求单源最短路径
设 S 为最短距离已确定的顶点集 (看作红点集),V-S 是最短距离尚未确定的顶点集 (看作绿点集)。
①初始化
初始化时,只有源点 s 的最短距离是已知的 (SD (s)=0),故红点集 S={s},蓝点集为空。
②重复以下工作,按路径长度递增次序产生各顶点最短路径 在当前蓝点集中选择一个最短距离最小的蓝点来扩充红点集,以保证算法按路径长度递增的次序产生各顶点的最短路径。当蓝点集中仅剩下最短距离为∞的蓝点,或者所有蓝点已扩充到红点集时,s 到所有顶点的最短路径就求出来了。
// 图的最短路径算法 | |
#define INFINITY 32768 /* 表示极大值,即∞*/ | |
typedef unsigned int WeightType; | |
typedef WeightType AdjType; | |
typedef SeqList VertexSet; | |
/* path [i] 中存放顶点 i 的当前最短路径。dist [i] 中存放顶点 i 的当前最短路径长度 */ | |
void ShortestPath_DJS(AdjMatrix g, int v0,WeightType dist[MAX_VERTEX_NUM],VertexSet path[MAX_VERTEX_NUM] ){ | |
VertexSet s; /* s 为已找到最短路径的终点集合 */ | |
/* 初始化 dist [i] 和 path [i] */ | |
for ( i =0;i<g.vexnum ;i++) { | |
InitList(&path[i]); | |
dist[i]=g.arcs[v0][i].adj; | |
if ( dist[i] < INFINITY){ | |
AddTail(&path[i], g.vertex[v0]); /* AddTail 是表尾添加操作 */ | |
AddTail(&path[i], g.vertex[i]); | |
} | |
} | |
InitList(&s); | |
AddTail(&s, g.vertex[v0]); /* 将 v0 看成第一个已找到最短路径的终点 */ | |
/* 求 v0 到其余 n-1 个顶点的最短路径 (n= g.vexnum)*/ | |
for ( t = 1; t<=g.vexnum-1; t++) { | |
min= INFINITY; | |
for ( i =0; i<g.vexnum;i++) | |
if (! Member(g.vertex[i], s) && dist[i]<min ) { | |
k =i; | |
min=dist[i]; | |
} | |
AddTail(&s, g.vertex[k]); | |
/* 修正 dist [i], i∈V-S*/ | |
for ( i =0; i<g.vexnum;i++) | |
if (!Member(g.vertex [i], s) && g.arcs[k][i].adj!= INFINITY && (dist[k]+ g.arcs [k][i].adj<dist[i])){ | |
dist[i]=dist[k]+ g.arcs [k][i].adj; | |
path[i]=path[k]; | |
AddTail(&path[i], g.vertex [i]); /* path[i]=path[k]∪{Vi} */ | |
} | |
} | |
} |
4. 求任意一对顶点间的最短路
佛罗伊德算法
设图 g 用邻接矩阵法表示,求图 g 中任意一对顶点 vi、、vj 间的的最短路径。(-1) 将 vi 到 vj 的最短的路径长度初始化为 g.arcs [i][j].adj,然后进行如下 n 次比较和修正:
(0) 在 vi、vj 间加入顶点 v0,比较 (vi,v0,vj) 和 (vi,vj) 的路径的长度,取其中较短的路径作为 vi 到 vj 的且中间顶点号不大于 0 的最短路径。
(1) 在 vi、vj 间加入顶点 v1,得到 (vi,…, v1) 和 (v1,…, vj),其中 (vi,…,v1) 是 vi 到 v1 的且中间顶点号不大于 0 的最短路径,(v1,…,vj) 是 v1 到 vj 的且中间顶点号不大于 0 的最短路径,这两条路径在上一步中已求出。将 (vi,…,v1,…,vj) 与上一步已求出的且 vi 到 vj 中间顶点号不大于 0 的最短路径比较,取其中较短的路径作为 vi 到 vj 的且中间顶点号不大于 1 的最短路径。
(2) 在 vi、vj 间加入顶点 v2,得 (vi,…,v2) 和 (v2,…,vj),其中 (vi,…,v2) 是 vi 到 v2 的且中间顶点号不大于 1 的最短路径,(v2,…,vj) 是 v2 到 vj 的且中间顶点号不大于 1 的最短路径,这两条路径在上一步中已求出。将 (vi,…,v2,…,vj) 与上一步已求出的且 vi 到 vj 中间顶点号不大于 1 的最短路径比较,取其中较短的路径作为 vi 到 vj 的且中间顶点号不大于 2 的最短路径。
………
依次类推,经过 n 次比较和修正,在第 (n-1) 步,将求得 vi 到 vj 的且中间顶点号不大于 n-1 的最短路径,这必是从 vi 到 vj 的最短路径。图 g 中所有顶点偶对 vi、vj 间的最短路径长度对应一个 n 阶方阵 D。在上述 n+1 步中, D 的值不断变化,对应一个 n 阶方阵序列。
// 弗洛伊德算法 | |
typedef SeqList VertexSet; | |
/* g 为带权有向图的邻接矩阵表示法, path [i][j] 为 vi 到 vj 的当前最短路径,dist [i][j] 为 vi 到 vj 的当前最短路径长度 */ | |
void ShortestPath_Floyd(AdjMatrix g,WeightType dist [MAX_VERTEX_NUM] [MAX_VERTEX_NUM],VertexSet path[MAX_VERTEX_NUM] [MAX_VERTEX_NUM] ){ | |
/* 初始化 dist [i][j] 和 path [i][j] */ | |
for (i=0; i<g.vexnumn; i++) | |
for (j =0;j<g.vexnum; j++){ | |
InitList(&path[i][j]); | |
dist[i][j]=g.arcs[i][j].adj; | |
if (dist[i][j]<INFINITY){ | |
AddTail(&path[i][j], g.vertex[i]); | |
AddTail(&path[i][j], g.vertex[j]); | |
} | |
} | |
for (k =0;k<g.vexnum;k++) | |
for (i =0;i<g.vexnum;i++) | |
for (j=0;j<g.vexnum;j++) | |
if (dist[i][k]+dist[k][j]<dist[i][j]){ | |
dist[i][j]=dist[i][k]+dist[k][j]; | |
paht[i][j]=JoinList(paht[i][k], paht[k][j]); | |
} /* JoinList 是合并线性表操作 */ | |
} |
7. 总结
(1) 基本概念:
图中顶点间的关系可以任意的,因此图是最复杂的非线性结构,它的表达力强。图具有有向图、无向图、连通图、强连通图、完全图、赋权图等多种类型。
(2) 图的存储结构:
图的存储方式一般有两类,用边的集合方式有邻接矩阵,链接方式有邻接表、十字链表、邻接多重表。邻接矩阵和邻接表是两种常用的存储结构,适用于有向图 (网) 和无向图 (网) 表示与处理。
(3) 图的基本操作:由于图中结点间可以是多对多的关系,为实现图的遍历必须设置访问标志数组,以防止走回路或未访问到。图的遍历规律有两种:深度优先遍历 DFS 和广度优先遍历 BFS。可用用邻接矩阵和邻接表实现深度优先遍历和广度优先遍历算法。深度优先遍历算法是以递归技术为支持,而广度优先遍历算法是以队列技术为支持。
(4) 图的应用:图的遍历算法是图应用的重要基础。求解生成树、最小生成树、连通分量,拓扑排序、关键路径、单源最短路径及所有顶点之间的最短路径的重要算法应用。