# 树

1. 定义

树 (tree) 是 n (n ≥ 0) 个结点的有限集合 T，T 为空时称为空树，否则满足如下条件:
(1) 有且仅有一个称为根 (root) 的结点；
(2) 其余结点可分为 m (m>=0) 个互不相交的有限集合 T1, T2, …, Tm, 且其中每一个集合本身又是一棵树，称之为根的子树 (subtree)。

2. 基本术语

1、结点：包含一个数据元素及若干指向其子树的分支。
2、边：连接两个结点的线段。
3、度：一个结点拥有的子树数称为该结点的度。
4、树的度：指该树中结点的最大度数。
5、叶子 (终端结点)：度为零的结点称为叶子。
6、分支结点 (非终端结点)：度不为零的结点。
7、内部结点：根结点 (开始结点) 之外的分支结点称为内部结点。
8、孩子和双亲：结点的子树的根称为该结点的孩子，相应的，该结点称为孩子的双亲。
9、兄弟：同一个双亲的孩子之间互称兄弟。
10、堂兄弟：双亲在同一层的结点互为堂兄弟。
11、祖先：一个结点的祖先是从根结点到该结点路径上所经过的所有结点。
12、子孙：一个结点的子孙则是以该结点为根的子树中所有的结点 (不包括该结点) 13、结点的层次：从根开始定义起，根为第一层，根的孩子为第二层。若某结点在第 l 层，则其子树的根就在第 l+1 层。
14、树的深度 (高度)：树中结点的最大层次称为树的深度。
15、有序树：树中每个结点的各子树看成从左到右有次序即不能互换称为有序树。
16、无序树：树中每个结点的各子树看成从左到右无次序称为无序树。
17、森林：m (m>=0) 棵互不相交的树的集合。对树中每个结点而言，其子树的集合即为森林。
18、树和森林的转换
树 ————> 森林：删去树的根。
森林 ———> 树：加上一个结点的根。

3. 基本操作：

① InitTree(Tree)： 将 Tree 初始化为一棵空树。
② DestoryTree(Tree)： 销毁树 Tree。
③ CreateTree(Tree)： 创建树 Tree。
④ TreeEmpty(Tree)： 若 Tree 为空，则返回 TRUE，否则返回 FALSE。
⑤ Root(Tree)： 返回树 Tree 的根。
⑥ Parent(Tree，x)： 树 Tree 存在，x 是 Tree 中的某个结点。若 x 为非根结点，则返回它的双亲，否则返回“空”。
⑦ FirstChild(Tree，x)： 树 Tree 存在，x 是 Tree 中的某个结点。若 x 为非叶子结点，则返回它的第一个孩子结点，否则返回“空”。
⑧ NextSibling(Tree，x)： 树 Tree 存在，x 是 Tree 中的某个结点。若 x 不是其双亲的最后一个孩子结点，则返回 x 后面的下一个兄弟结点，否则返回“空”。
⑨ InsertChild(Tree，p，Child)： 树 Tree 存在，p 指向 Tree 中某个结点，非空树 Āhild与 Tree 不相交。将 Child 插入 Tree 中，做 p 所指向结点的子树。
⑩ DeleteChild(Tree，p，i)： 树 Tree 存在，p 指向 Tree 中某个结点，1≤i≤d，d为 p 所指向结点的度。删除 Tree 中 p 所指向结点的第 i 棵子树。
11 TraverseTree(Tree，Visit())： 树 Tree 存在，Visit()是对结点进行访问的函数。按照某种次序对树 Tree 的每个结点调用 Visit()函数访问一次且最多一次。若 Visit()失败，则操作失败。

4. 存储结构

1) 双亲表示法：
这种方法用一组连续的空间来存储树中的结点，在保存每个结点的同时附设一个指示器来指 示其双亲结点在表中的位置。
节点结构 : Data|Parent

2) 孩子表示法：
这种方法通常是把每个结点的孩子结点排列起来，构成一个单链表，称为孩子链表。n 个结 点共有 n 个孩子链表 (叶子结点的孩子链表为空表)，而 n 个结点的数据和 n 个孩子链表的 头指针又组成一个顺序表。

3) 孩子兄弟表示法：(二叉链表表示法)
这种表示法又称为树的二叉表示法，或者二叉链表表示法，即以二叉链表作为树的存储结构。 链表中每个结点设有两个链域，分别指向该结点的第一个孩子结点和下一个兄弟 (右兄弟) 结点。
节点结构 : FirstChild|Data|Nextsibling

//1) 双亲表示法

#define MAX 100

typedef struct TNode{

	DataType data;

	int parent;

} TNode;

//2) 孩子表示法

 /* 孩子链表结点的定义 */

typedef struct ChildNode{

	int Child; 					/* 该孩子结点在线性表中的位置 */

	struct ChildNode * next;	/* 指向下一个孩子结点的指针 */

}ChildNode;

/* 顺序表结点的结构定义 */

typedef struct{

	DataType data; 				/* 结点的信息 */

	ChildNode * FirstChild ;	/* 指向孩子链表的头指针 */

} DataNode;

/* 树的定义 */

typedef struct{ 

	DataNode nodes[MAX]; 		/* 顺序表 */

	int root; 					/* 该树的根结点在线性表中的位置 */

	int num; 					/* 该树的结点个数 */

}ChildTree;

//3) 孩子兄弟表示法

typedef struct CSNode{

    DataType data; 				/* 结点信息 */

	Struct CSNode *FirstChild; 	/* 第一个孩子 */

	Struct CSNode *Nextsibling; /* 下一个兄弟 */

} CSNode, *CSTree;

5. 相互转换

1. 树转换为二叉树
⑴ 树中所有相邻兄弟之间加一条连线。
⑵ 对树中的每个结点，只保留其与第一个孩子结点之间的连线， 删去其与其他孩子结点之间的连线。
⑶ 以树的根结点为轴心，将整棵树顺时针旋转一定的角度，使之结构层次分明。 树做这样的转换所构成的二叉树是惟一的。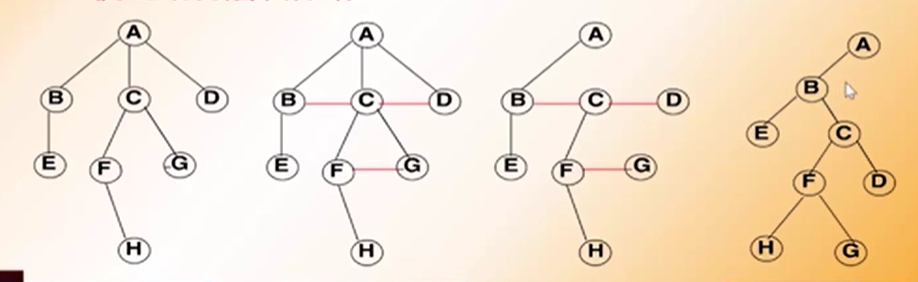

2. 二叉树还原为树或森林
(1) 若某结点是其双亲的左孩子，则把该结点的右孩子、右孩子的右孩子、…… 都与 该结点的双亲结点用线连起来。
(2) 删掉原二叉树中所有双亲结点与右孩子结点的连线。
(3) 整理由前两步所得到的树或森林，使之结构层次分明。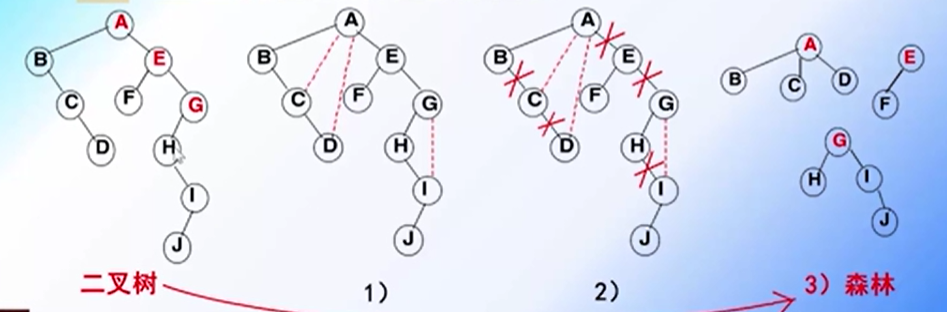

3. 森林转换为二叉树
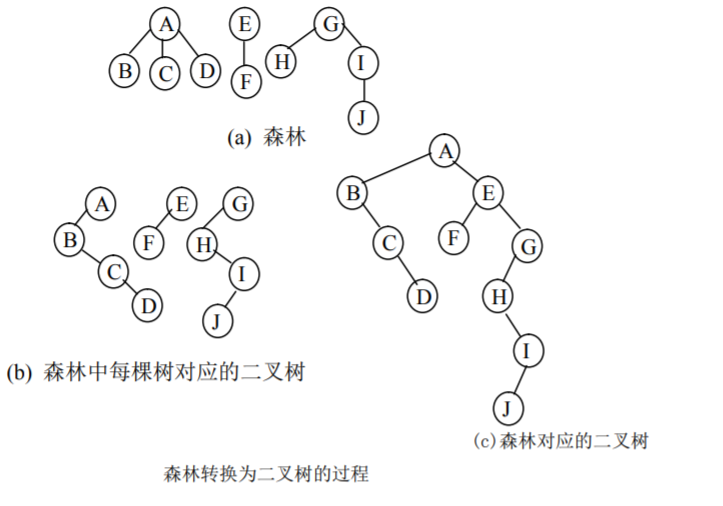
(1) 将森林中的每棵树转换成相应的二叉树。
(2) 第一棵二叉树不动，从第二棵二叉树开始，依次把后一棵二叉树的根结点作为前 一棵二叉树根结点的右孩子，当所有二叉树连在一起后，所得到的二叉树就是由 森林转换得到的二叉树。

6. 树与森林的遍历

1．树的遍历
树的遍历方法主要有以下两种：

(1) 先根遍历：
若树非空，则遍历方法为：
① 访问根结点。
② 从左到右，依次先根遍历根结点的每一棵子树。
(2) 后根遍历：
若树非空，则遍历方法为：
①从左到右，依次后根遍历根结点的每一棵子树。
②访问根结点。

// 方法一

void RootFirst(CSTree root){

	if (root!=NULL){

        Visit(root ->data); /* 访问根结点 */

		p= root-> FirstChild;

		while (p!=NULL){

            RootFirst( p ); /* 访问以 p 为根的子树 */

			p = p -> Nextsibling;

		}

	}

}

// 方法二

void RootFirst(CSTree root){

	if (root!=NULL){

		Visit (root ->data); /* 访问根结点 */

		RootFirst (root->FirstChild); /* 先根遍历首子树 */

		RootFirst (root->Nextsibling); /* 先根遍历兄弟树 */

	}

}

2. 森林的遍历

森林的遍历方法主要有以下三种：
(1) 先序遍历 若森林非空，则遍历方法为：
①访问森林中第一棵树的根结点。
②先序遍历第一棵树的根结点的子树森林。
③先序遍历除去第一棵树之后剩余的树构成的森林。 例如，右图中森林的先序遍历序列为 ABCDEFGHIJ。
(2) 中序遍历 若森林非空，则遍历方法为：
①中序遍历森林中第一棵树的根结点的子树森林。
②访问第一棵树的根结点。
③中序遍历除去第一棵树之后剩余的树构成的森林。 例如，右图中森林的中序遍历序列为 BCDAFEHJIG。
(3) 后序遍历 若森林非空，则遍历方法为：
①后序遍历森林中第一棵树的根结点的子树森林。
② 后序遍历除去第一棵树之后剩余的树构成的森林。
③访问第一棵树的根结点。 例如，右图中森林的后序遍历序列为 DCBFJIHGEA。