二叉树 - 树 - 数据结构 - 计算机科学 | Twelveeee = 十二的编程笔记 = hello world

# 二叉树

# 1. 定义

把满足以下两个条件的树型结构叫做二叉树 (Binary Tree)：
(1) 每个结点的度都不大于 2；
(2) 每个结点的孩子结点次序不能任意颠倒。

由此定义可看出，一个二叉树中的每个结点只能含有 0、1 或 2 个孩子，而且每个孩子有左右之分。位于左边的孩子叫做左孩子，位于右边的孩子叫做右孩子。

基本形态：
(a) 空二叉树
(b) 只有根结点的二叉树
(c) 只有左子树的二叉树
(d) 左右子树均非空的二叉树
(e) 只有右子树的二叉树

# 2. 性质

1. 二叉树的第 i 层上至多有 2^(i-1)(i >=1) 个结点。
2. 深度为 k 的二叉树中至多 (2^k)-1 个结点。
3. 对任何一棵二叉树 T，如果其终端结点数为 n0，度为 2 的结点数为 n2，则 n0＝n2＋1。

满二叉树：
定义：如果一个二叉树深度为 K，结点数为 2k-1，则称为满二叉树
特点：每一层上的结点数都是最大结点数。

完全二叉树：
定义：指深度为 k 的，有 n 个结点的，且每一个结点都与深度为 k 的满二叉树中编号从 1 至 n 的结点一一对应。
特点:
1) 叶子结点只可能在层次最大的两层上出现；
2) 对任一结点，若其右分支下的子孙的最大层次为 L，则其左分支下的子孙的最大层次必为 L 或 L+1。
即：完全二叉树可以不满，但是少的结点只能从满二叉树的最下层、最右边少起。
(个人认为，就是满二叉树的完整前半部分)

4. 具有 n 个结点的完全二叉树的深度 k 为└log2n┘+1。

5：如果对一棵有 n 个结点的完全二叉树 (其深度为└log2 (n)┘+1) 的结点按层序编号 (从第一层到第└log2 (n)┘+1 层，每层从左到右)，则对任意结点 i (0≤i≤n), 有：

如果 i=1，则结点 i 是二叉树的根，无双亲；若 i>1，则它的双亲结点的编号为└i/2┘。
若 2i>n，则结点 i 无左孩子 (结点 i 为叶子结点)；否则其左孩子编号为 2i 。
3) 若 2i+1>n，则结点 i 无右孩子；否则其右孩子编号为 2i+1。

# 3. 存储结构

1. 顺序存储结构:

用一组连续的存储单元存放二叉树中的结点

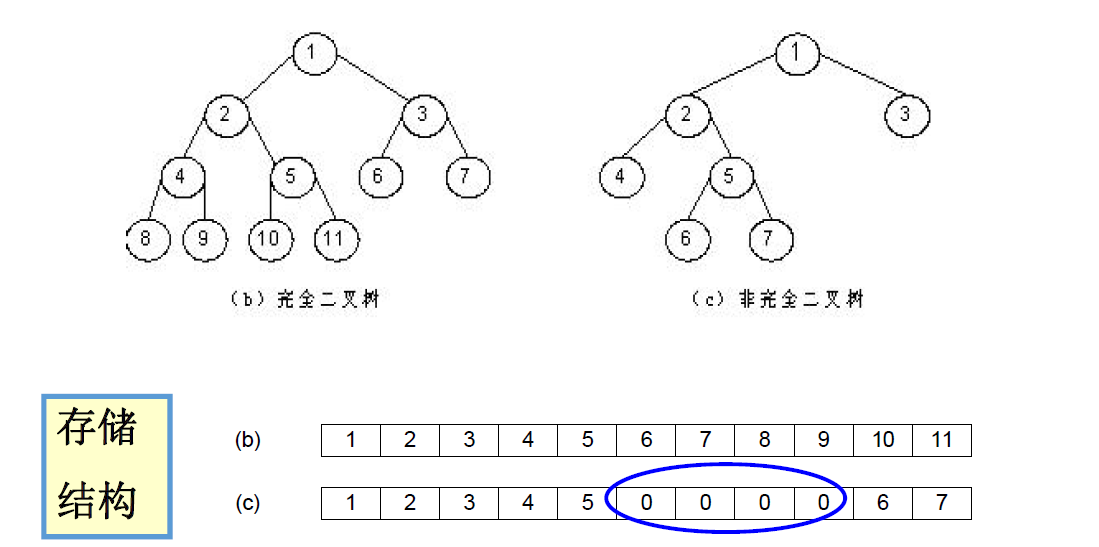
优点：适用于满二叉树和完全二叉树，按结点从上至下，从左到右顺序存放，结点序号唯一反映出结点间逻辑关系，又可用数组下标值确定结点位置。

缺点：对一般二叉树，需增加许多空结点将一棵二叉树改造成完全二叉树，浪费大量存储空间。(否则数组元素下标间不能反映各结点间逻辑关系)

2. 链式存储结构
二叉链表：每个结点由数据域、左指针域和右指针域组成。

	typedef struct node{
	Datatype data;
	struct node Lchild,Rchild;
	}BiTNode;
	typedef BiTNode * BinTree ;
	// 注意：BiTNode 是结点类型，BinTree 是指向 BiTNode 的指针类型

三叉链表：增加一个指向其双亲结点的指针域。

# 4. 遍历二叉树

1. 遍历：是指沿着某条搜索路线，依次对树中每个结点均做一次且做一次访问。
2. 目的：非线性结构线性化。
二叉树是非线性结构，经过一次完整遍历，可将各结点的非线性排列变为某种意义的线性序列。

3. 方式：

一棵二叉树的组成:
根结点 D (访问根结点)
左子树 L (遍历左子树)
右子树 R (遍历右子树)

(1) 先序遍历 (NLR/DLR)
(2) 中序遍历 (LDR/LNR)
(3) 后序遍历 (LRD/LRN)

	// 先序遍历的递归算法:
	void NLR(BinTree T){
	if(T!=null){
	printf(“%c”,T->data);
	NLR(T->Lchild);
	NLR(T->Rchild);
	}
	}
	// 中序遍历的递归算法:
	void LNR(BinTree T){
	if(T!=null){
	LNR(T->Lchild);
	printf(“%c”,T->data);
	LNR(T->Rchild);
	}
	}
	// 后序遍历的递归算法:
	void LRN (BinTree T){
	if(T!=null){
	LRN (T->Lchild);
	LRN (T->Rchild);
	printf(“%c”,T->data);
	}
	}

4. 应用

	//1) 建立二叉链表
	void CreateBiTree(BiTree &T) {
	// 按先序次序输入二叉树中结点的值 (一个字符)，空格字符表示空树，
	// 构造二又链表表示的二叉树 T
	char ch;
	scanf(&ch);
	if(ch ==’’) T = NULL;
	else{
	if(!(T = (BiTNode *)malloc(sizeof(BiTNode)))) exit(OVERFLOW);
	T->data = ch; // 生成根结点
	CreateBiTree(T -> lchild); // 构造左子树
	CreateBiTree(T -> rchild) // 构造右子树
	}
	return OK;
	}// CreateBiTree

	//2) 求二叉树的结点个数
	int count(BiTree T){
	int lcount,rcount;
	if (T==NULL) return 0;
	else{
	lcount = count(T -> lchild);
	rcount = count(T -> rchild);
	return lcount + rcount +1;
	}
	}

	//3) 求二叉树叶子结点的个数
	int countleaf(BiTree T){
	int lcount,rcount;
	if (T==NULL) return 0;
	else{
	lcount = countleaf(T -> lchild);
	rcount = countleaf(T -> rchild);
	if(T->lchild==NULL && T->rchild==NULL) return lcount + rcount +1;
	else return lcount + rcount;
	}
	}

	//4) 求二叉树度为 1 的结点的个数 (上面那个改)
	int countdeg1(BiTree T){
	int lcount,rcount;
	if (T==NULL) return 0;
	else{
	lcount = countdeg1(T -> lchild);
	rcount = countdeg1(T -> rchild);
	if((T->lchild != NULL && T->rchild == NULL)\|\|(T->lchild ==
	NULL && T->rchild != NULL)) return lcount + rcount +1;
	else return (lcount + rcount);
	}}

	//5) 计算二叉树的深度
	int BiTDepth(BiTree T){
	int ldep,rdep;
	if (T==NULL) return 0;
	else{
	ldep=BiTDepth(T->lchild)+1;
	rdep=BiTDepth(T->rchild)+1;
	return ldep>rdep?ldep:rdep;
	}
	}

	//6) 复制二叉树
	Status CopyBiTree(BiTree &T, BiTree &T1){
	BiTree p;
	if(T){
	p=new BiTNode;
	if(!p) return ERROR;
	p->data=T->data;
	T1=p;
	CopyBiTree(T->lchild,T1->lchild);
	CopyBiTree(T->rchild,T1->rchild);
	}
	else T1=T;
	return OK;
	}

	//7) 按竖向树状打印的二叉树
	void PrintTree(BiTree bt, int nLayer) {
	if(bt = =NULL) return;
	PrintTree(bt ->RChild, nLayer+1);
	for(int i=0; i<nLayer; i++)
	printf(“ ”);
	printf(“%c\n”, bt ->data); /* 按逆中序输出结点，用层深决定的左、右位置 */
	PrintTree(bt ->LChild , nLayer+1);
	}

基于栈的递归消除

	// 中序遍历二叉树的非递归算法 (c) (调用栈操作的函数)
	void InOrder(BiTree root){
	InitStack (&S);
	p=root;
	while(p!=NULL \|\| !IsEmpty(S)){
	if(p!=NULL){ /* 根指针进栈，遍历左子树 */
	Push(&S,p);
	p=p->LChild;
	}else{
	/* 根指针退栈，访问根结点，遍历右子树 */
	Pop(&S,&p);
	Visit(p->data);
	p=p->RChild;
	}
	}
	}
	// 时间复杂度 O (n) 循环次数为 n+(n+1)=2n+1,
	// 空间复杂度 O (k) 所需栈的空间最多等于二叉树深度 K 乘以每个结点所需空间数

# 5. 线索二叉树

1. 基本概念

线索：指向结点前驱和后继的指针，叫做线索。
线索链表：以这种结点结构构成的二叉链表作为二叉树的存储结构，叫做线索链表。
线索二叉树 (Threaded Binary Tree)：加上线索的二叉树称之为线索二叉树。
线索化：对二叉树以某种次序遍历使其变为线索二叉树的过程叫做线索化。
通俗一点，没有左孩子的给他加前驱，没右孩子的给他加后继 (先左再右遍历)

线索二叉树结点结构 LChild|Ltag|Data|Rtag|RChild

Ltag=0 LChild 域指示结点的左孩子
Ltag=1 LChild 域指示结点的遍历前驱
Rtag=0 RChild 域指示结点的右孩子
Rtag=1 RChild 域指示结点的遍历后继

2. 线索化

	/* 对 root 所指的二叉树进行中序线索化，其中 pre 始终指向刚访问过的结点，其初值为 NULL */
	void Inthread(BiTree root){
	if (root!=NULL){
	/* 线索化左子树 */
	Inthread(root->LChild);

	/* 置前驱线索 */
	if (root->LChild==NULL){
	root->Ltag=1;
	root->LChild=pre;
	}

	/* 置后继线索 */
	if (pre!=NULL&& pre->RChild==NULL) {
	pre-> RChild=root;
	pre->Rtag=1;
	}
	/* 当前访问结点为下一个访问结点的前驱 */
	pre=root;
	Inthread(root->RChild); /* 线索化右子树 */
	}
	}

3. 查找前驱后继节点

	/* 在中序线索二叉树中查找 p 的中序前驱，并用 pre 指针返回结果 */
	BiTNode InPre(BiTNode p){
	if(p->Ltag==1) pre= p->LChild; /* 直接利用线索 */
	else{ /* 在 p 的左子树中查找 “最右下端” 结点 */
	for(q= p->LChild;q->Rtag==0;q=q->RChild);
	pre=q;
	}
	return(pre);
	}

	/* 在中序线索二叉树中查找 p 的中序后继结点，并用 Next 指针返回结果 */
	BiTNode InNext(BiTNode p){
	if (p->Rtag==1) Next= p-> RChild; /* 直接利用线索 */
	else{ /* 在 p 的右子树中查找 “最左下端” 结点 */
	if(p->RChild!=NULL){
	for(q= p->RChild; q->Ltag==0 ;q=q->LChild );
	Next=q;
	}else Next = NULL;
	}
	return(Next)
	}
	// 遍历中序二叉线索树
	void TInOrder(BiTree Bt){
	BITNode *p;
	P=InFirst(Bt);
	While(p){
	Visit(p);
	p = InNext(p);
	}
	}

数据结构