# 4. 选择类排序
选择排序 (Selection Sort) 的基本思想是:每一趟从待排序的记录中选出关键字最小的记录,顺序放在已排好序的子文件的最后,直到全部记录排序完毕。
# 1. 简单选择排序
基本思想
第一趟,从 n 个记录中找出关键字最小的记录与第一个记录交换;
第二趟,从第二个记录开始的 n-1 个记录中再选出关键码最小的记录与第二个记录交换;
第 i 趟,则从第 i 个记录开始的 n-i+1 个记录中选出关键字最小的记录与第 i 个记录交换,直到整个序列按关键字有序。
这种操作进行 n-1 次,但每一次的待排元素个数比上一次少一个。
void SelectSort(SqList &L){ | |
for(i=0;i<=L->length-1;i++){ | |
min=i; // 假设最小值下标为 i | |
for(j=i+1; j<L->length-1; j++)if(L->data[min]>L->data[j]) | |
min=j; | |
if(i!=min){ | |
temp=L->data[i]; | |
L->data[i]=L->data[min]; | |
L->data[min]=temp; | |
} | |
} | |
} |
性能分析:
时间复杂度 O (n2)
空间效率:O (1)
不稳定
# 2. 树型选择排序
树型选择排序也称作锦标赛排序。基本思想是先把待排序的 n 个记录的关键字两两进行比较,取出较小者,然后再在 n /2 个较小者中,采用同样的方法进行比较选出每两个中的较小者,如此反复,直至选出最小关键字记录为止。
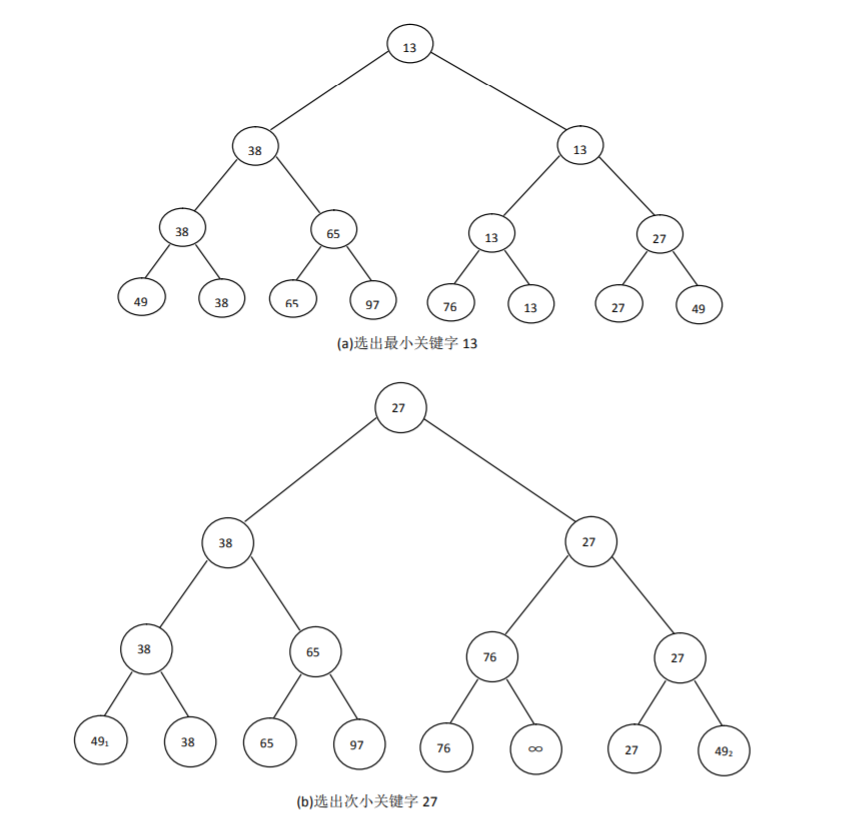
性能分析:
时间复杂度 O (nlog2n)
# 3. 堆排序
大根堆:这棵完全二叉树中任意结点的关键字大于或者等于其左孩子和右孩子的关键字
小根堆:这棵完全二叉树中任意结点的关键字小于或者等于其左孩子和右孩子的关键字
基本思想
将序列构造成一棵完全二叉树
把这棵普通的完全二叉树改造成堆,便可获取最小值(最大值)
输出最小(大)值
将最后一个结点放到输出结点的位置,再次改造,直至输出所有结点
重建堆
首先将与堆相应的完全二叉树根结点中的记录移出,该记录称为待调整记录。此时根结点相当于空结点,从空结点的左、右子中选出一个关键字较小的记录,如果该记录的关键字小于待调整记录的关键字,则将该记录上移至空结点中。
/* 假设r[k..m] 是以r[k] 为根的完全二叉树,且分别以r[2k] 和r[2k+1] 为根的左、右 | |
子树为大根堆,调整 r [k],使整个序列 r [k..m] 满足堆的性质 */ | |
void sift(RecordType r[], int k,int m){ | |
t= r[k] ; /* 暂存 “根” 记录 r [k] */ | |
x=r[k].key ; | |
i=k ; | |
j=2*i ; | |
finished=FALSE ; | |
while( j<=m && ! finished ){ | |
/* 若存在右子树,且右子树根的关键字大,则沿右分支 “筛选” */ | |
if (j<m && r[j].key< r[j+1].key ) j=j+1; | |
if ( x>= r[j].key) finished=TRUE ; /* 筛选完毕 */ | |
else { | |
r[i] = r[j] ; | |
i=j ; | |
j=2*i ; | |
} /* 继续筛选 */ | |
} | |
r[i] =t ; /* r [k] 填入到恰当的位置 */ | |
} |
建初堆
将一个任意序列看成是对应的完全二叉树,由于叶结点可以视为单元素的堆,因而可以反复利用上述调整堆算法(“筛选” 法),自底向上逐层把所有子树调整为堆,直到将整个完全二叉树调整为堆。
/* 对记录数组 r 建堆,length 为数组的长度 */ | |
void crt_heap(RecordType r[], int length ){ | |
n= length; | |
for(i=n/2 ; i>= 1 ; --i) /* 自第 n / 2 个记录开始进行筛选建堆 */ | |
sift(r,i,n) ; | |
} |
性能分析:
时间复杂度 O (nlog2n))
空间效率:O (1)
不稳定