# 2. 插入排序
基本思想:将一个元素记录按其应用的位置插入
到已排好序的序列中。依据寻找插入位置的方法不同,插入排序分为:
直接插入排序;折半插入排序;希尔插入排序;表插入排序。
# 1. 直接插入排序
基本思想:
插入 Ri 时,R1,R2,…,Ri-1 已排好,用 Ri 的关键字与 Ri-1,Ri-2,…,R1 比较,找到插入位置。即把一个记录插入到已排好序的有序表中。
/* 对记录数组 r 做直接插入排序,length 为数组中待排序记录的数目 */ | |
void InsSort(RecordType r[], int length){ | |
for ( i=2 ; i<=length ; i++ ){ | |
r[0]=r[i]; j=i-1; /* 将待插入记录存放到监视哨 r [0] 中 */ | |
while (r[0].key< r[j].key ){ /* 寻找插入位置 */ | |
r[j+1]= r[j]; j=j-1; | |
} | |
r[j+1]=r[0]; /* 将待插入记录插入到已排序的序列中 */ | |
} | |
} /* InsSort */ |
性能分析:
时间复杂度 O(n2)
空间复杂度 O(1)
稳定
# 2. 折半插入排序
(二分法插入排序)
基本思想:
设在顺序表中有一个记录序列 R [1], R [2], …, R [n]。其中,R [1], R [2], …, R [i-1] 是已经排好序的记录。在插入 R [i] 时,利用折半搜索法寻找 R [i] 的插入位置。
/* 对记录数组 r 进行折半插入排序,length 为数组的长度 */ | |
void BinSort (RecordType r[], int length){ | |
for ( i=2 ; i<=length ; ++i ){ | |
x= r[i]; | |
low=1; | |
high=i-1; | |
while (low<=high ){ /* 确定插入位置 */ | |
mid=(low+high) / 2; | |
if ( x.key< r[mid].key ) high=mid-1; | |
else low=mid+1; | |
} | |
for ( j=i-1 ; j>= low; --j ) r[j+1]= r[j]; /* 记录依次向后移动 */ | |
r[low]=x; | |
/* 插入记录 */ | |
} | |
}/*BinSort*/ |
性能分析:
时间复杂度 O(nlog2n)
空间复杂度 O(1)
稳定
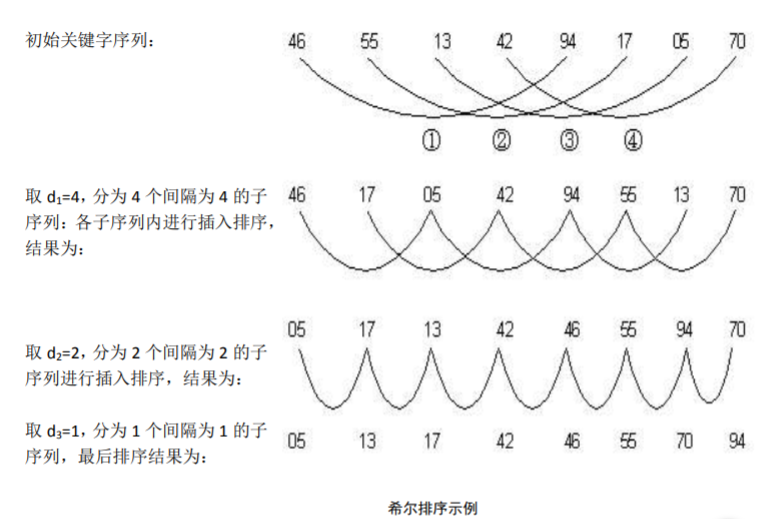
# 3. 希尔排序
基本思想
先将待排序记录序列分割成若干序列,分别进行直接插入排序;待整个序列中的记录基本有序后,再全体进行一次直接插入排序。
/* 对记录数组 r 做一趟希尔插入排序,length 为数组的长度,delta 为增量 */ | |
void ShellInsert(RecordType r[], int length, int delta){ | |
for(i=1+delta ;i<= length; i++) /* 1+delta 为第一个子序列的第二个元素的下标 */ | |
if(r[i].key < r[i-delta].key){ | |
r[0]= r[i]; /* 备份 r [i] (不做监视哨) */ | |
for(j=i-delta; j>0 &&r[0].key < r[j].key ; j-=delta) | |
r[j+delta]= r[j]; | |
r[j+delta]= r[0]; | |
} | |
}/*ShellInsert*/ | |
/* 对记录数组 r 做希尔排序,length 为数组 r 的长度,delta 为增量数组,n 为 delta [] 的长度 */ | |
void ShellSort(RecordType r[], int length, int delta[], int n){ | |
for(i=0 ; i<=n-1; ++i) | |
ShellInsert(r, Length, delta[i]); | |
} |
性能分析:
时间复杂度 O(n^1.5)
空间复杂度 O(1)
不稳定