# 2. 基于线性表的查找法
# 1. 顺序查找法
基本思想:从表的一端开始逐个进行记录的关键字和给定值的比较。
储存结构:
// 顺序结构数据类型的定义: | |
#define LIST_SIZE 20 | |
typedef struct { | |
KeyType key; | |
OtherType other_data; | |
} RecordType; | |
typedef struct { | |
RecordType r[LIST_SIZE+1]; /* r [0] 为工作单元 */ | |
int length; | |
} RecordList; |
算法实现:
/* 不用 “监视哨” 法,在顺序表中查找关键字等于 k 的元素 */ | |
int SeqSearch(RecordList l, KeyType k){ | |
i=l.length; | |
while (i>=1&&l.r[i].key!=k) i--; | |
if (i>=1) return(i) | |
else return (0); | |
} |
行能分析:
平均比较次数(设等概率 Pi=1/n)
查找成功时: ASLs = Pi*(n-i+1)=(1+2+3+….+n)/n = (n+1)/2
查找不成功时:ASLsm =(n+1)
顺序查找的平均查找长度为: ASL=((n+1)/2+(n+1))/2= 3 (n+1)/4
优点:算法简单,对表结构无任何要求,关键字是否有序。
缺点:查找效率低,n 较大时不宜采用。
用平均查找长度(ASL)分析顺序查找算法的性能。假设列表长度为 n,那么查找第 i 个数据元素时需进行 n-i+1 次比较,即 Ci=n-i+1。又假设查找每个数据元素的概率相等,即 Pi=1/n,则顺序查找算法的平均查找长度为:
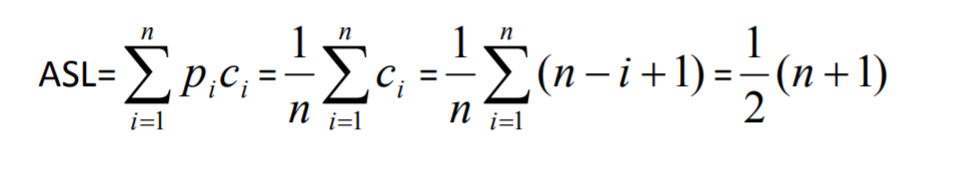
# 2. 折半查找法
折半查找法又称为二分查找法,这种方法对待查找的列表有两个要求:
(1)必须采用顺序存储结构;(2)必须按关键字大小有序排列。
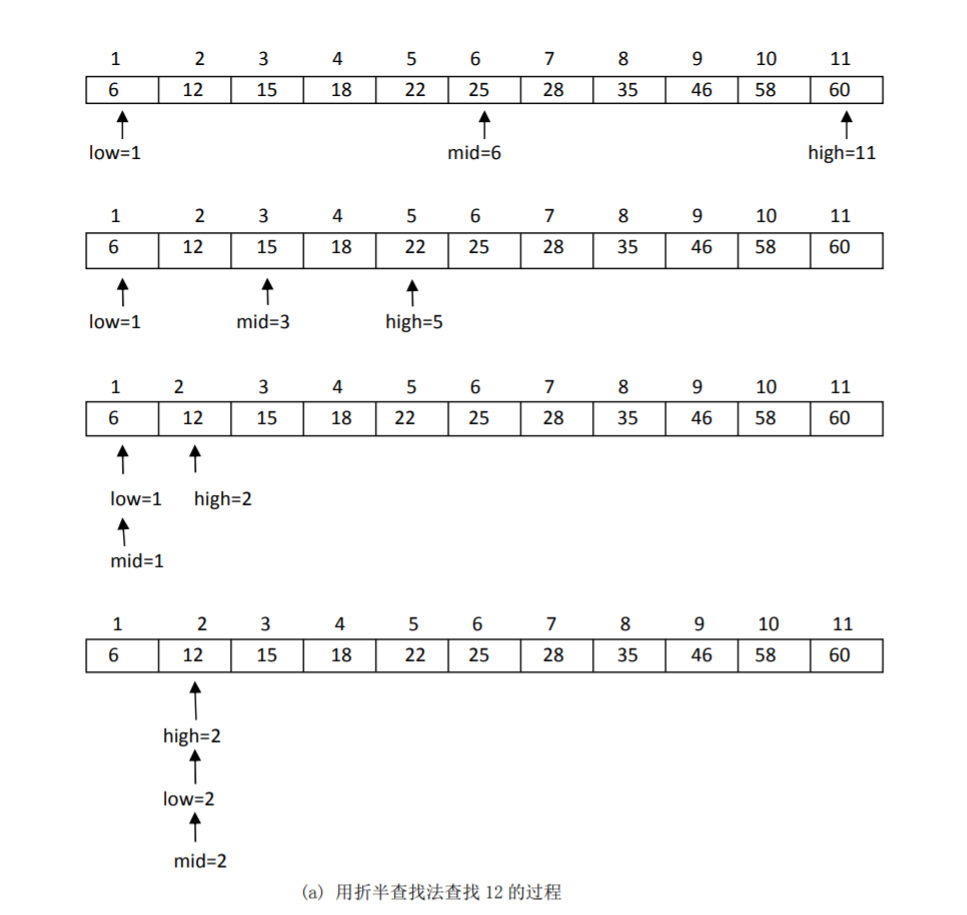
基本思想:
将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置记录将表分成前、后两个子表,如果中间位置记录的关键字大于查找关键字,则进一步查找前一子表,否则进一步查找后一子表。
算法实现:
/* 在有序表 l 中折半查找其关键字等于 k 的元素,若找到,则函数值为该元素在表中的位置 */ | |
int BinSrch (RecordList l, KeyType k){ | |
low=1 ; | |
high=l.length;/* 置区间初值 */ | |
while ( low<=high){ | |
mid=(low+high)/2; | |
if (k==l.r[mid]. key) return(mid);/* 找到待查元素 */ | |
else if (k<l.r[mid]. key) high=mid-1;/* 未找到,则继续在前半区间进行查找 */ | |
else low=mid+1;/* 继续在后半区间进行查找 */ | |
} | |
return (0); | |
} |
行能分析:
折半查找方法的优点是比较次数少,查找速度快,平均性能好;其缺点是要求待查表为有序表,且插入删除困难。因此,折半查找方法适用于不经常变动而查找频繁的有序列表。
ASL =(n+1)/n log2(n+1)-1 = log2(n+1)-1
# 3. 分块查找法
分块查找法要求将列表组织成以下索引顺序结构:
首先将列表分成若干个块(子表)。一般情况下,块的长度均匀,最后一块可以不满。每块中元素任意排列,即块内无序,但块与块之间有序。
构造一个索引表。其中每个索引项对应一个块并记录每块的起始位置,以及每块中的最大关键字(或最小关键字)。索引表按关键字有序排列。
分块查找的基本过程如下:
⑴首先,将待查关键字 K 与索引表中的关键字进行比较,以确定待查记录所在的块。具体的可用顺序查找法或折半查找法进行。
⑵进一步用顺序查找法,在相应块内查找关键字为 K 的元素
| 顺序查找 | 折半查找 | 分块查找 | |
|---|---|---|---|
| ASL | 最大 | 最小 | 两者之间 |
| 表结构 | 有序表、无序表 | 有序表 | 分块有序表 |
| 存储结构 | 顺序存储结构、线性链表 | 顺序存储结构 | 顺序存储结构、线性链表 |