矩阵的压缩存储

# 4. 稀疏矩阵

1. 定义

假设在 mn 的矩阵中，有 t 个元素不为零。令 δ=t/mn，称 δ 为矩阵的稀疏因子。通常认为 δ≤0.05 时称为稀疏矩阵。

2. 稀疏矩阵的压缩存储思想

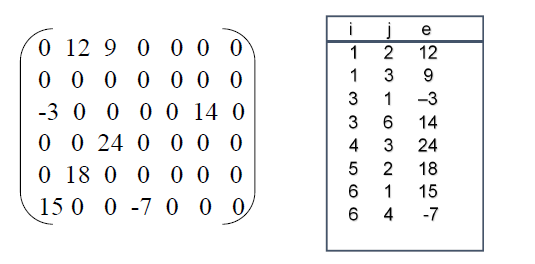
按照压缩存储的概念，为了节省存储单元，可以只存储稀疏矩阵的非零元素。因此在存储非零元素的同时，还必须存储非零元素所在的行号、列号，才能迅速确定一个非零元素是矩阵中的哪一个元素。其中每一个非零元素所在的行号、列号和值组成一个三元组 (i，j，aij)，并由此三元组惟一确定。
稀疏矩阵进行压缩存储通常有两类方法：
・顺序存储
・链式存储

3. 稀疏矩阵的三元组顺序表存储

假设以顺序存储结构来表示三元组表，则可得稀疏矩阵的
一种压缩存储方式，我们称之为三元组顺序表。

例：

	typedef struct{
	int i,j; // 该非零元素的行下标和列下标
	ElemType e; // 非零元素值
	}Triple; // 三元组类型

	typedef struct{
	Triple data[MAXSIZE+1] // 非零元三元组表，data [0] 未用
	int mu, nu, tu; // 矩阵的行数、列数和非零元素的个数
	}TSMatrix; // 三元组表的顺序存储类型

4. 稀疏矩阵的十字链表存储

在十字链表中，矩阵的每一个非零元素用一个结点表示，该结点除了 (row,col,value) 以外，还要有以下两个链域:
right: 用于链接同一行中的下一个非零元素。
down: 用于链接同一列中的下一个非零元素。

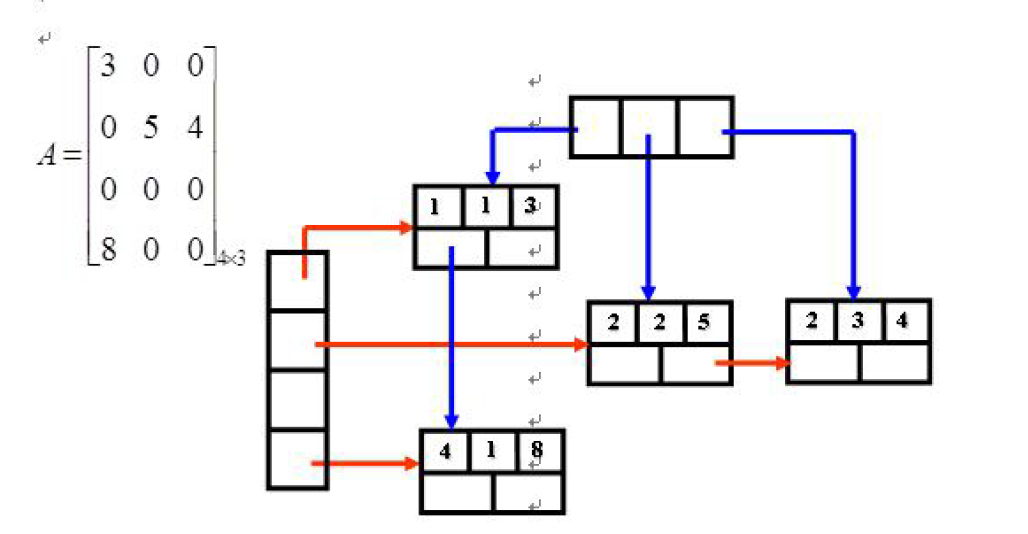
在十字链表中，同一行的非零元素通过 right 域链接成一个单链表。同一列的非零元素通过 down 域链接成一个单链表。这样，矩阵中任一非零元素 M [i][ j] 所对应的结点既处在第 i 行的行链表上，又处在第 j 列的列链表上，这好像是处在一个十字交叉路口上，所以称其为十字链表。同时再附设一个存放所有行链表的头指针的一维数组和一个存放所有列链表的头指针的一维数组。

	typedef struct OLNode{
	int row, col; /* 非零元素的行和列下标 */
	ElementType value;
	struct OLNode * right,down; / 非零元素所在行表、列表的后继链域 */
	}OLNode; *OLink;

	typedef struct{
	OLink * row_head, col_head; / 行、列链表的头指针向量 */
	int m, n, len; /* 稀疏矩阵的行数、列数、非零元素的个数 */
	}CrossList;

转置运算

转置运算是一种最简单的矩阵运算。对于一个 mn 的矩阵 M，它的转置矩阵 T 是一个 nm 的矩阵，且

T(i,j)=M(j,i)，1≤i≤n，1≤j≤m

显然，一个稀疏矩阵的转置矩阵仍然是稀疏矩阵。

	// 稀疏矩阵转置经典算法
	void TransMatrix(ElementType source[m][n], ElementType dest[n][m]){
	/source 和 dest 分别为被转置的矩阵和转置以后的矩阵 (用二维数组表示)/
	int i, j;
	for(i=0;i<m;i++)
	for (j=0;j< n;j++)
	dest[j][i]=source[i] [j] ;
	}

三元组

	// 三元组表实现稀疏矩阵的转置
	void TransposeTSMatrix(TSMatrix A, TSMatrix * B){
	/* 把矩阵 A 转置到 B 所指向的矩阵中去。矩阵用三元组表表示 */
	int i , j, k ;
	B->m= A.n ;
	B->n= A.m ;
	B->len= A.len ;
	if(B->len>0){
	j=1; /j 为辅助计数器，记录转置后的三元组在三元组表 B 中的下标值 /
	for(k=1; k<=A.n; k++) /* 扫描三元组表 A 共 A.n 次，每次寻找列值为 k 的三元组进行转置 */
	for(i=1; i<=A.len; i++)
	if(A.data[i].col==k){
	B->data[j].row=A.data[i].col;
	B->data[j].col=A.data[i].row;
	B->data[j].e=A.data[i].e;
	j++; }/* 计数器 j 加 1，指向本行下一个转置后元素的位置下标 */
	}/* if (B->len>0) 的结束 */
	}/* end of TransposeTSMatrix */

	// 稀疏矩阵 “一次定位快速转置” 算法
	void FastTransposeTSMatrix (TSMatrix A, TSMatrix * B){
	/* 基于矩阵的三元组表示，采用 “一次定位快速转置” 法，将矩阵 A 转置为矩阵 B*/
	int col , t , p，q;
	int num[MAXSIZE], position[MAXSIZE] ;
	B->len= A.len ;
	B->n= A.m ;
	B->m= A.n ;
	if(B->len){
	for(col=1;col<=A.n;col++)num[col]=0;

	/* 采用数组下标计数法计算每一列的非零元素的个数 */
	for(t=1;t<=A.len;t++)num[A.data[t].col]++;
	position[1]=1;

	/* 求 col 列中第一个非零元素在 B.data [ ] 中的正确位置 */
	for(col=2;col<=A.n;col++)position[col]=position[col-1]+num[col-1];
	for(p=1;p<=A.len;p++){/* 将被转置矩阵的三元组表 A 从头至尾扫描一次，实现矩阵转置 */
	col=A.data[p].col; q=position[col];
	B->data[q].row=A.data[p].col;
	B->data[q]..col=A.data[p].row;
	B->data[q].e=A.data[p].e;
	/position [col] 加 1，指向下一个列号为 col 的非零元素在三元组表 B 中的存放位置 /
	position[col]++;
	}
	}
	}

数据结构

# 4. 稀疏矩阵

对称矩阵